Binary search trees explained

• Binary tree definitions
• Binary search tree
  • Example
• Balanced trees with O(log n) time complexity
• Tree algorithms
  • Inorder traversal
  • Search
  • Insert

Binary tree definitions

A binary tree is a data structure most easily described by recursion.

A binary tree

• is either empty,
• or consists of a node (also known as the root of the tree) and two subtrees, the left and right subtree, which are also binary trees.

A node with two empty subtrees is called a leaf.

If p is a node and q is the root of p’s subtree, we say that p is the parent of q and that q is a child of p. Two nodes with the same parents are called siblings.

The set of ancestors if the node n is defined recursively by these two rules:

• n is an ancestor of n.
• If q is a child of p and q is an ancestor of n, then p is an ancestor of n as well.

The set of ancestors to the node n form a path from n to the root of the tree.

The depth of a node is the number of element on the path from the node to the root.

The depth of a tree is defined to be the largest depth of any node in the tree. The empty tree has depth 0.

Binary search tree

A binary search tree is a binary tree where each node contains a value from a well-ordered set.

For each node n in a binary search tree the following invariants hold.

• Every node in the left subtree of n contains a value which is smaller than the value in the node n.
• Every node in the right subtree of n contains a value which is larger than the value in the node n.

Example

This binary tree has 9 nodes and depth 4.

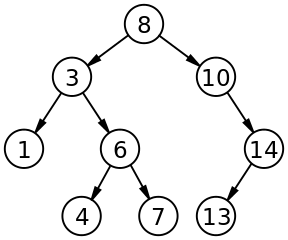
The root of the tree contains the value 8. The leaf values are 1, 4, 7 and 13.

• Each node in the left subtree has a value smaller than  8,
• while each node in the right subtree has a value larger than  8.

In fact, this is a binary search tree, since the corresponding invariant holds for each node in the tree.

Balanced trees with O(log n) time complexity

We say that a tree is well-balanced if each node in the tree has two subtrees with roughly the same number of nodes. It’s possible to show that a well-balanced tree with n nodes has depth O(log n).

If we can manage to keep a binary search tree well-balanced, we get an ordered data structure with O(log n) worst-case time complexity for all basic operations: lookup, addition and removal.

There are several, more or less complicated, strategies to keep a binary search tree well-balanced.

• AVL trees came first,
• Red-black trees are used by Java’s TreeSet,
• Treaps, randomized binary search trees, are simple and elegant.

See the Treaps: randomized search trees article for a full description of treaps.

In this text we only present pseudocode for some basic operations on unbalanced binary search trees.

Warning: An unbalanced tree can be very inefficient. In the most extreme case, for example when all left subtrees are empty, the tree degrades into a singly linked list.

Tree algorithms

Inorder traversal

An inorder traversal of a binary search tree visits the nodes in sorted order.

// Visit all nodes of a binary search tree in sorted order.
Algorithm inorder(root)
    if root is empty
        // do nothing
    else
        inorder(root.left)
        // do something with root
        inorder(root.right)

Search

It’s pretty straightforward to implement the find operation in a binary search tree with iteration, but to keep things simple, here is a recursive version.

// Returns true if the value is found in the tree.
Algorithm find(value, root)
    if root is empty
        return false
    if value = root.value
        return true
    if value < root.value
        return find(value, root.left)    
    else
        return find(value, root.right)

Insert

To implement an algorithm that changes the structure of a tree, it’s convenient to define a function that takes the root of the old tree as input, and returns the root of new updated tree.

// Adds a new node and returns the root of the updated tree.
Algorithm insert(node, root)
    if root is empty
        return node
    if node.value = root.value
        // do nothing, element already in tree
    else if node.value < root.value
        root.left ← insert(node, root.left)
    else
        root.right ← insert(node, root.right)
    return root