Radix sorting basics

yourbasic.org

Radix sorting is a simple and efficient sorting method that sometimes outperforms comparison-based algorithms.

Bucket sort
LSD radix sort
MSD radix sort

Radix sort is a non-comparative sorting algorithm for sorting numbers or strings. It distributes elements into buckets according to the digits of the numbers or the characters of the strings.

Bucket sort

Bucket sort is the basic building block of most radix sorting schemes. It solves the special case of sorting n integers drawn from a small set {0, 1, …, m-1}.

Bucket sort maintains one bucket for each possible key value, puts the elements in their respective buckets, and then collects the elements during a traversal of the buckets.

Implementation

Perhaps the most obvious implementation is to use an array of linked lists to represent the m buckets. By maintaining pointers to both the head and tail of each list we can insert the elements at the end of a list in constant time, and assure that the sort is stable.

Counting sort

Another possibility, often referred to as counting sort, is to use an array of counters, where each counter indicates the number of elements in each bucket. The final position of the first element in each bucket is computed with a prefix sum computation. With this information available it is possible to permute the n elements into sorted order in O(n) time. One drawback of this scheme is that each character has to be read twice, one time during the counting and one time during the permutation.

In-place permutation

The simplest way to permute the elements is to move them into a new array. It is also possible to perform the permutation in place as illustrated in this picture.

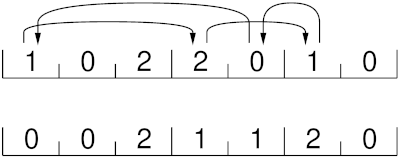
If the first element isn’t 0 we move this element into its correct position, and remove the element that resides in that position; if this element equals 0 we are done, otherwise we continue to displace elements until we eventually find a 0 element, which can be placed in the first slot. This procedure is repeated for the next element that has not yet found its correct place.

To perform this sequence of displacements we need to keep track of the current point of insertion for each bucket. This can be arranged using a pointer array of size m. The initial values of this array are computed as the prefix sums of the counter array. Observe that this in-place permutation scheme produces a sorting algorithm that is not stable.

Optimization

Clustering is present in many kinds of data. We can take advantage of this by treating consecutive elements with a common value as a single unit when moving them into a bucket. Using a linked-list representation it is possible to move this sublist of identical elements in constant time.

Analysis

Bucket sort inspects each element a constant number of times and visits each bucket once, hence it runs in Θ(n + m) time.

The linked list implementation uses Θ(n + m) extra space: Θ(n) space is used to implement the linked list and Θ(m) is needed for the buckets.

With in-place permutation, it is possible to implement bucket sort with only Θ(m) extra space. However, this implementation is not stable.

LSD radix sort

Bucket sort is a feasible alternative only if the elements to be sorted take their values from a restricted domain. For bigger numbers we may divide the sort into several stages, using bucket sort at each stage. The most common approach is to start with the least significant digit (LSD). This method was used already to sort punched cards. The algorithm is often referred to as LSD radix sort, straight radix sort, or bottom-up radix sort.

The algorithm, in its basic form, requires all strings to be of equal length. It works as follows.

Split the strings into groups according to their last character and arrange the groups in ascending order.
Apply the algorithm recursively on all strings, disregarding the last character of each string.

After step i of the algorithm, the input strings will be properly sorted according to their last i characters.

Implementation

The sorting subroutine is typically implemented using bucket sort. Other sorting subroutines may of course also be used, as long as they are stable.

To implement a string sorting algorithm efficiently we should not move the strings themselves but only pointers to them. In this way, each string movement is guaranteed to take constant time.

Optimization

In many cases we are able to choose the size of the alphabet (the radix):

For numbers we are free too choose any base: from binary to decimal, or much larger.
For strings we may look at one character at a time, or combine several characters into one.

When choosing the radix we are faced with a fundamental choice: a large alphabet reduces the total number of passes but increases the total number of buckets that must be inspected.

Analysis

The running time of LSD radix sort is a function of the number of strings n, the number of buckets m, and the length l of the strings. During the bucketing phase each of the n characters is inspected once and during the rebuilding each of the m buckets is visited once. This procedure is repeated l times and hence the running time is Θ(l(n + m)).

MSD radix sort

The major weakness of LSD radix sort is that it needs to inspect all characters of the input. Another, perhaps more natural, alternative is to scan the strings starting with the most significant digit (MSD) and only inspects the distinguishing prefixes. This algorithm is known as MSD radix sort or top-down radix sort. The special case where the alphabet is binary is sometimes referred to as radix-exchange sort. The algorithm works as follows.

Split the strings into groups according to their first character and arrange the groups in ascending order.
Apply the algorithm recursively on each group separately, disregarding the first character of each string. Groups containing only one string need no further processing.

After step i of the algorithm, the input strings will be properly sorted according to their first i characters.

Implementation

Once again, bucket sort is typically used to implement the sorting at each step. In this case we can use the in-place version of bucket sort, but then the resulting algorithm will of course be unstable.

We want to avoid using a new bucket table for each splitting. This can be arranged if we use an explicit stack to keep track of the flow of computation. The last bucket is treated first and the other sublists to be sorted are pushed on the stack.

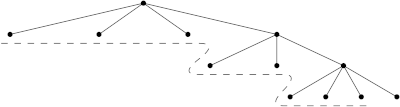
The sublists on the stack that are waiting to be sorted are suggested by the dotted line in this figure.

Optimizations

In MSD radix sort the groups may become small while the cost of bucket sort remains proportional to the size of the alphabet. This fragmentation problem can be mitigated by swapping to another sorting algorithm when only a small number of elements remain in a group.

Another drawback is that the stack can be sizable. In fact, in the basic version of the algorithm the stack may contain one entry for each key.

We suggest a simple way to lessen this problem. If both the list on the top of the stack and the list in turn to be pushed onto the stack are sorted there is no need to allocate another stack record. We can simply append one list to the end of the other.

This technique is applicable if the algorithm switches to a comparison-based algorithm to sort short subsequences. If we switch when at most k elements remain in a group, each stack entry will contain at least k elements and hence the total size of the stack will be at most n/k.

In practice, the stack will typically be much smaller. Not only does this simple optimization give a considerable reduction of the stack size, it is also likely to improve the running time.

Analysis

The algorithm inspects each distinguishing character once, and each string at least once. Hence the algorithm has time complexity at least O(n + S), where S is the total number of characters of the distinguishing prefixes, i.e. the characters that must be inspected to sort the strings:

To compute the number of buckets that are visited we observe that bucketing takes place at each internal node of the corresponding execution tree. The number of nodes in this tree could be as large as Θ(S) and hence the worst-case time complexity is Θ(n + mS).

In practice, when using the optimization techniques discussed above, the performance is often much better than could be expected from this worst-case time bound. In particular, the technique to revert to a simpler sorting algorithm when only a small constant number of elements remain is often very effective, even though it does not improve the asymptotic bound.