Amortized time complexity
Amortized analysis is used for algorithms that have expensive operations that happen only rarely.
Amortized complexity analysis is most commonly used with data structures that have state that persists between operations. The basic idea is that an expensive operation can alter the state so that the worst case cannot occur again for a long time, thus amortizing its cost.
Let T1, T2, …, Tk be the complexities of a sequence of operations on a data structure. The amortized complexity of a single operation in this sequence is (T1 + T2 + …+ Tk) / k.
Example: a dynamic array
In a dynamic array, elements are stored at the start of an underlying fixed array, and the remaining positions are unused.
// Append x to the end of a dynamic array a.
algorithm append(x, a):
if a.size == a.capacity
b ← new array with twice the capacity of a
copy a into b
a ← b
a[a.size] ← x
a.size++
Here’s a view of the memory when appending the elements 2, 7, 1, 3, 8, 4 to an inititally empty array with capacity 2.
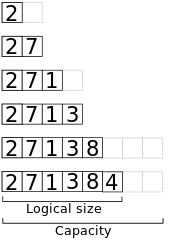
Worst-case time
The worst-case time complexity for appending an element to an array of length n, using this algorithm, is Θ(n). If the array is full, the algorithm allocates a new array of length 2n, and then copies the elements from the old array into the new one.
Cleary this result is overly pessimistic. The following n append operations will be much cheaper – each of them will run in constant time since the newly allocated array has room for all the new elements.
Amortized time
An amortized time analysis gives a much better understanding of the algorithm.
Consider a sequence of n append operations, where we start with an array of length 1. A careful analysis shows that the total time of these operations is only Θ(n).
- There will be a total of n constant-time assignment and increment operations.
- The resizing will happen only at operation 1, 2, 4, …, 2k, for a total of 1 + 2 + 4 + …+ 2k = 2·2k - 1 constant-time element copy operations. Since 2k ≤ n, this is at most 2n - 1.
Hence, the amortized time complexity for a single append operation is Θ(1).
More on algorithm analysis
Time complexity: Count your steps
Share this page:
