Time complexity of array/list operations [Java, Python]

To write fast code, you must know the difference between constant and linear time array operations.

Accidentally inefficient list code with quadratic time complexity is very common and can be hard to spot, but when the list grows your code grinds to a halt.

This text takes a detailed look at the performance of basic array operations and discusses alternatives to a standard array. It also includes cheat sheets of expen­sive list operations in Java and Python.

Array basics

An array is the most fundamental collection data type. It consists of elements of a single type laid out sequentially in memory. You can access any element in constant time by integer indexing.

Arrays are available in all major languages. In Java you can either use []-notation, or the more expressive ArrayList class. In Python, the list data type is imple­mented as an array.

Performance

In general, arrays have excellent performance. To optimize array performance is a major goal of memory hardware design and OS memory management.

• You can read or write a list item by referring to its index in constant time.
• However, some array operations – such as add, remove, and search – can be quite expensive, with worst-case linear time complexity.

Dynamic array

In a dynamic array, elements are stored at the start of an underlying fixed array, and the remaining positions are unused.

• If there is room left, elements can be added at the end in constant time.
• If there is no remaining positions, the underlying fixed-sized array needs to be increased in size.

Here’s a view of the memory when appending the elements 2, 7, 1, 3, 8, 4 to an initially empty dynamic array with capacity 2.

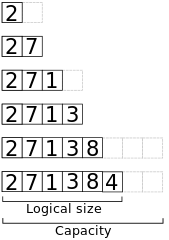
The time to append an element is linear in the worst case, since it involves allocating new memory and copying each element.

However, if we expand the array by a constant proportion, e.g. by doubling its size, the total time to insert n elements will be O(n), and we say that each insertion takes constant amortized time.

See Amortized time complexity for more on how to analyze data structures that have expensive operations that happen only rarely.

Expensive list operations

To add or remove an element at a specified index can be expensive, since all elements after the index must be shifted. The worst-case time complexity is linear.

Similarly, searching for an element for an element can be expensive, since you may need to scan the entire array.

In this Python code example, the linear-time pop(0) call, which deletes the first element of a list, leads to highly inefficient code:

Warning: This code has quadratic time complexity. It runs in time Θ(n²), where n is the initial length of the list a. This means that the program is useful only for short lists, with at most a few thousand elements.

while len(a) > 0:
	foo = a.pop(0)

To avoid this type of performance problems, you need to know the difference between constant and linear time list operations.

Expensive Java ArrayList methods

The following ArrayList methods operate on a subset of the elements, but still have time complexity that depends on the size n of the list.

Note: add(E element) takes constant amortized time, even though the worst-case time is linear.

Expensive Python list operations

The following Python list operations operate on a subset of the elements, but still have time complexity that depends on n = len(a).

Note: a.append(x) takes constant amortized time, even though the worst-case time is linear.

Alternatives

No other data structure can compete with the efficiency of array indexing and array iteration. However, you may need to take a different approach if other operations are performance critical.

Maps and dictionaries

The hash table, often in the form of a map or a dictionary, is the most commonly used alternative to an array. It implements an unordered collection of key-value pairs, where each key is unique.

• Hash tables offer a combination of efficient search, add and delete operations.
• All of these operations run in expected constant time. The time complexity for the add operation is amortized.

In Java, hash tables are part of the standard library (HashSet and HashMap). Many modern languages, such as Python and Go, have built-in dictionaries and maps implemented by hash tables.

Sorted arrays

If search is important for performance, you may want to use a sorted array.

• In a sorted array, you can use binary search, which runs in worst-case logarithmic time.
• However, it can be expensive to add a new element to a sorted array: the element needs to be inserted in its right place.

The Java Arrays class contains implementations of binary search, Python offers a similar bisect algorithm, and Go also has several binary search methods.

Linked lists

If you need to repeatedly add or remove elements at the start or end of a list, you may want to consider a linked list.

• In a singly linked list you can add elements at both ends in constant time, and also remove the first element in constant time.
• In a doubly linked list, you can also remove the last element in constant time.
• However, indexing is very expensive. To find an element at a given index you need to traverse the list.

The Java LinkedList class implements a doubly linked list, Python offers a deque, and Go also has a list package.

Binary search trees

Balanced binary search trees store items in sorted order and offer effi­cient lookup, addi­tion and remo­val of items.

• Most basic operations (e.g. add, delete, find and min) run in logarithmic time.

In Java, search trees are part of the standard library (TreeSet and TreeMap), while Python and Go don’t support them out of the box.

Share this page: