Las Vegas vs. Monte Carlo algorithms

A Las Vegas algorithm is a randomized algorithm that always gives the correct result but gambles with resources.

Monte Carlo simulations are a broad class of algorithms that use repeated random sampling to obtain numerical results.

• Monte Carlo simulations are typically used to simulate the behaviour of other systems.
• Monte Carlo algorithms, on the other hand, are randomized algorithms whose output may be incorrect with a certain, typically small, probability.

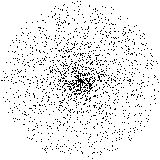
Random point in circle (Las Vegas)

It’s easy and convenient to compute a random point in a circle with a Las Vegas algorithm.

The idea is to first generate a point (x, y), with -1 < x < 1 and -1 < y < 1. If this point happens to fall within the unit circle we keep it, otherwise we throw it away and try again.

This algorithm obviously gives the correct result, but it gambles with the number of calls to the random number generator.

// Point returns a random point in the unit circle.
func Point() (x, y float64) {
	for { // This loop runs 4/π times on average.
		x = 2*rand.Float64() - 1
		y = 2*rand.Float64() - 1
		if x*x+y*y < 1 {
			return
		}
	}
}

Warning: Note that the following function gives an uneven distri­bution. It’s more likely to produce a point close to the middle of the circle.

func Point() (x, y float64) {
	r := rand.Float64()
	θ := 2 * math.Pi * rand.Float64()
	return r * math.Cos(θ), r * math.Sin(θ)
}

Approximate value of π (Monte Carlo)

If points (x, y), with -1 < x < 1 and -1 < y < 1, are placed randomly, the ratio of points that fall within the unit circle will be close to π/4.

A Monte Carlo simulation would randomly place points in the square and use the percentage of points inside the circle to estimate the value of π.

const n = 100000
count := 0
for i := 0; i < n; i++ {
	x := 2*rand.Float64() - 1
	y := 2*rand.Float64() - 1
	if x*x+y*y < 1 {
		count++
	}
}
fmt.Println(4 * float64(count) / float64(n)) // 3.1484

Share this page: