Hash tables explained [step-by-step example]

• Basics
• Hashing with chaining (simplified example)
• Realistic hash function example
• Resizing in constant amortized time

Basics

Hash tables are used to implement map and set data structures in most common programming languages. In C++ and Java they are part of the standard libraries, while Python and Go have builtin dictionaries and maps.

A hash table is an unordered collection of key-value pairs, where each key is unique.

Hash tables offer a combination of efficient lookup, insert and delete operations. Neither arrays nor linked lists can achieve this:

• a lookup in an unsorted array takes linear worst-case time;
• in a sorted array, a lookup using binary search is very fast, but insertions become inefficient;
• in a linked list an insertion can be efficient, but lookups take linear time.

Hashing with chaining (simplified example)

The most common hash table implementation uses chaining with linked lists to resolve collisions. This combines the best properties of arrays and linked lists.

Hash table operations are performed in two steps:

• A key is converted into an integer index by using a hash function.
• This index decides the linked list where the key-value pair record belongs.

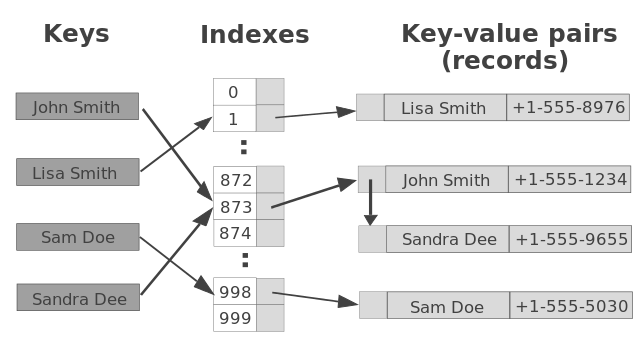
Let’s start with a somewhat simplified example: a data structure that can store up to 1000 records with random integer keys.

To distribute the data evenly, we use several short lists. All records with keys that end with 000 belong to one list, those with keys that end with 001 belong to another one, and so on. There is a total of 1000 such lists. This structure can be represented as an array of lists:

var table = new LinkedList[1000]

where LinkedList denotes a linked list of key-value pairs.

Inserting a new record (key, value) is a two-step procedure:

• we extract the three last digits of the key, hash = key % 1000,
• and then insert the key and its value into the list located at table[hash].

hash = key % 1000
table[hash].AddFirst(key, value)

This is a constant time operation.

A lookup is implemented by

value = table[key%1000].Find(key)

Since the keys are random, there will be roughly the same number of records in each list. Since there are 1000 lists and at most 1000 records, there will likely be very few records in the list table[key%1000] and therefore the lookup operation will be fast.

The average time complexity of both the lookup and insert operations is O(1). Using the same technique, deletion can also be implemented in constant average time.

Realistic hash function example

We want to generalize this basic idea to more complicated keys that aren’t evenly distributed. The number of records in each list must remain small, and the records must be evenly distributed over the lists. To achieve this we just need to change the hash function, the function which selects the list where a key belongs.

The hash function in the example above is hash = key % 1000. It takes a key (a positive integer) as input and produces a number in the interval 0..999.

In general, a hash function is a function from E to 0..size-1, where E is the set of all possible keys, and size is the number of entry points in the hash table. We want this function to be uniform: it should map the expected inputs as evenly as possible over its output range.

Java’s implementation of hash functions for strings is a good example. The hashCode method in the String class computes the value

s[0]·31^n-1 + s[1]·31^n-2 + … + s[n-1]

using int arithmetic, where s[i] is the i:th character of the string, and n is the length of the string.

This method can be used as a hash function like this:

hash = Math.abs(s.hashCode() % size)

where size is the number of entry points in the hash table.

Note that this function

• depends on all characters in the string,
• and that the value changes when we change the order of the characters.

Two properties that should hold for a good hash function.

Resizing in constant amortized time

The efficiency of a hash table depends on the fact that the table size is proportional to the number of records. If the number of records is not known in advance, the table must be resized when the lists become too long:

• a new larger table is allocated,
• each record is removed from the old table,
• and inserted into the new table.

If the table size is increased by a constant factor for each resizing, i.e. by doubling its size, this strategy gives amortized constant time performance for insertions.

For more on the performance of this strategy, see Amortized time complexity.

Share this page: