Your basic int: a most powerful data type

yourbasic.org

The int data type is generic, effective, simple and efficient.

Introduction

Every kid can spot an integer number, and every programmer is familiar with the int data type. Still we frequently forget how powerful an integer can be.

Resources

This text comes with four Go example libraries:

Generic graph data

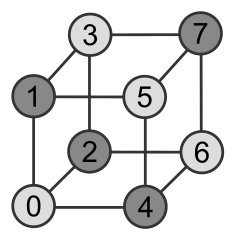
Graph

Cubical graph with vertex colors

Since graphs are used to model countless types of relations and processes in varied kinds of systems and settings, there is no telling what kind of data a generic graph library will encounter; both vertices and edges can have labels attached to them. Should we use parametric polymorphism or perhaps a pointer to the top of a type hierarchy?

It’s easy to forget that an integer may be the preferred choice. Here is a solution from the graph package.

All algorithms operate on directed graphs with
a fixed number of vertices, labeled from 0 to n-1,
and edges with integer cost.

Since vertices are represented by integers, it’s easy to add any kind of vertex data on the side. For example, this generic implementation of breadth-first search uses an array of booleans, visited, to keep track of which vertices have been visited.

// BFS traverses g in breadth-first order starting at v.
// When the algorithm follows an edge (v, w) and finds
// a previously unvisited vertex w, it calls do(v, w, c)
// with c equal to the cost of the edge (v, w).
func BFS(g Iterator, v int, do func(v, w int, c int64)) {
	visited := make([]bool, g.Order())
	visited[v] = true
	for queue := []int{v}; len(queue) > 0; {
		v := queue[0]
		queue = queue[1:]
		g.Visit(v, func(w int, c int64) (skip bool) {
			if visited[w] {
				return
			}
			do(v, w, c)
			visited[w] = true
			queue = append(queue, w)
			return
		})
	}
}

Code from bfs.go

Effective searching and sorting

Some of the most effective search and sort algorithms are implemented by bit manipulation done with bitwise integer operators. These operators operate, often in parallel, on the single bits of an integer. Even though they don’t form a Turing-complete set of operations, they can still be surprisingly effective.

The standard set of bitwise operators, found in almost every CPU, includes the bitwise NOT, AND, OR and XOR instructions; plus a collection of shift and rotate instructions. A bit count instruction, often known as popcnt, is also quite common.

Needles in huge haystacks

The Hamming distance between two integers, the number of positions at which the corresponding bits are different, is an effective way to estimate similarity. It can be computed using just one xor and one popcnt instruction.

Hamming distance

The Hamming distance between adjacent vertices in a cubical graph is one.

Rumor has it that organizations who are sifting through huge amounts of data prefer to buy CPUs that come with a bit count instruction. As a case in point, the Zen microarchitecture from AMD supports no less than four popcnt instructions per clock cycle.

Bit count

If the CPU doesn’t have a native bit count operation, popcnt can still be implemented quite efficiently using the more common bitwise operators. Here is a fun code sample from the bit package.

// Count returns the number of nonzero bits in w.
func Count(w uint64) int {
	// “Software Optimization Guide for AMD64 Processors”, Section 8.6.
	const maxw = 1<<64 - 1
	const bpw = 64

	// Compute the count for each 2-bit group.
	// Example using 16-bit word w = 00,01,10,11,00,01,10,11
	// w - (w>>1) & 01,01,01,01,01,01,01,01 = 00,01,01,10,00,01,01,10
	w -= (w >> 1) & (maxw / 3)

	// Add the count of adjacent 2-bit groups and store in 4-bit groups:
	// w & 0011,0011,0011,0011 + w>>2 & 0011,0011,0011,0011 = 0001,0011,0001,0011
	w = w&(maxw/15*3) + (w>>2)&(maxw/15*3)

	// Add the count of adjacent 4-bit groups and store in 8-bit groups:
	// (w + w>>4) & 00001111,00001111 = 00000100,00000100
	w += w >> 4
	w &= maxw / 255 * 15

	// Add all 8-bit counts with a multiplication and a shift:
	// (w * 00000001,00000001) >> 8 = 00001000
	w *= maxw / 255
	w >>= (bpw/8 - 1) * 8
	return int(w)
}

Code from funcs.go

As of Go 1.9, a bit count function is available in package math/bits. On most architectures functions in this package are recognized by the compiler and treated as intrinsics for additional performance. The Bitwise operators cheat sheet tells more about bit manipulation in Go.

Fast sorting

Radix sort also uses bit manipulation to good effect. For string sorting, a carefully implemented radix sort can be considerably faster than Quicksort, sometimes more than twice as fast. A discussion of MSD radix sort, its implementation and a comparison with other well-known sorting algorithms can be found in Implementing radixsort.

Bitwise operators are also crucial in the implementation of the fastest known integer sorting algorithm. It sorts n integers in O(n log log n) worst-case time on a unit-cost RAM machine, the standard computational model in theoretical computer science.

See The fastest sorting algorithm? for a complete description of this algorithm.

Simple sets

A bit set, or bit array, must be the simplest data structure in town. It’s just an array of integers, where the bit at position k is one whenever k belongs to the set.

Even though it’s simple, a bit set can be quite powerful. Because it uses bit-level parallelism, limits memory access, and plays nicely with the data cache, it tends to be very efficient and often outperforms other set data structures.

Memory consumption isn’t too shabby either. If you have a gigabyte of RAM to spare, you can story a set of integer elements in the range 0 to 8,589,934,591.

Sieve of Eratosthenes

Eratosthenes

Eratosthenes of Cyrene

This code snippet implements the sieve of Eratosthenes (with an optimization suggested by tege). It uses a bit set implementation from the bit package to generate the set of all primes less than n in O(n log log n) time. Try it with n equal to a few hundred millions and be pleasantly surprised.

sieve := bit.New().AddRange(2, n)
for k := 4; k < n; k += 2 {
    sieve.Delete(k)
}
sqrtN := int(math.Sqrt(n))
for p := 3; p <= sqrtN; p = sieve.Next(p) {
	for k := p * p; k < n; k += 2 * p {
		sieve.Delete(k)
	}
}

A fly in the ointment

The code above doesn’t guard against integer overflow. If n is too close to the maximum representable value of an int, the index variable k will eventually wrap around and become negative.

Efficient filtering

Hash functions are yet another triumph for the integer data type. They are worth a tribute of their own, but in this section we will just take them for granted. If we combine a bit array with a set of hash functions we get a Bloom filter, a probabilistic data structure used to test set membership.

This data structure tells whether an element may be in a set, or definitely isn’t. The only possible errors are false positives: a search for a nonexistent element can give an incorrect answer. With more elements in the filter, the error rate increases.

Bloom filters are both fast and space-efficient. However, elements can only be added, not removed.

Content distribution networks use them to avoid caching one-hit wonders, files that are seen only once. Web browsers use them to check for potentially harmful URLs.

This piece of code, from package bloom, shows a typical Bloom filter use case.

// A Bloom filter with room for at most 100000 elements.
// The error rate for the filter is less than 1/200.
blacklist := bloom.New(10000, 200)

// Add an element to the filter.
url := "https://rascal.com"
blacklist.Add(url) 

// Test for membership.
if blacklist.Test(url) {
	fmt.Println(url, "may be blacklisted.")
} else {
	fmt.Println(url, "has not been added to our blacklist.")
}
https://rascal.com may be blacklisted.

Implementation

An empty Bloom filter is a bit array of m bits, all set to 0. There are also k different hash functions, each of which maps a set element to one of the m bit positions.

Here is a Bloom filter with three elements x, y and z. It consists of 18 bits and uses 3 hash functions. The colored arrows point to the bits that the elements of the set are mapped to.

Bloom filter

The element w definitely isn’t in the set, since it hashes to a bit position containing 0.

The colored arrows point to the bits that the elements of the set {x, y, z} are mapped to. The element w is not in the set, because it hashes to a bit position containing 0.

Share this page: