Functional programming in Go [case study]

yourbasic.org/golang

A graph implementation based entirely on functions

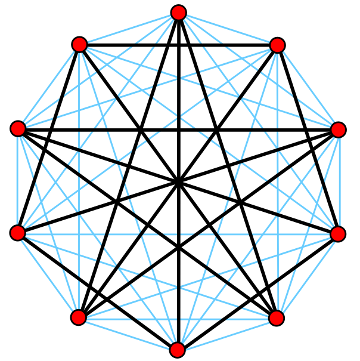
The Petersen graph and its complement

Introduction

This text is about the implementation of a Go tool based entirely on functions – the API contains only immutable data types, and the code is built on top of a struct with five func fields.

It’s a tool for building virtual graphs. In a virtual graph no vertices or edges are stored in memory, they are instead computed as needed. The tool is part of a larger library of generic graph algorithms:

the package graph contains the basic graph library and
the subpackage graph/build is the tool for building virtual graphs.

There is an online reference for the build tool at godoc.org.

The Petersen graph

Let’s start with an example, the Petersen graph. To describe this graph in a conventional graph library, you would typically need to enumerate the edges…

{0, 1}, {0, 4}, {0, 5}, {1, 2}, {1, 6}, {2, 3}, {2, 7}, {3, 4},
{3, 8}, {4, 9}, {5, 7}, {5, 8}, {6, 8}, {6, 9}, and {7, 9}

…in one way or another.

However, if you ask a mathematician to describe the Petersen graph, her answer would clearly be very different. Perhaps she would say:

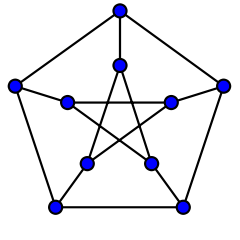
You get a Petersen graph if you draw a pentagon with a pentagram inside, with five spokes.

Petersen graph

This example from the graph/build documentation corresponds to the mathematical description.

// Build a Petersen graph.
pentagon := build.Cycle(5)
pentagram := pentagon.Complement()
petersen := pentagon.Match(pentagram, build.AllEdges())

As you can see, the Cycle, Complement and Match functions implement basic concepts in graph theory: we start with a cycle graph of order 5, compute its complement, and then combine these two graphs by matching their vertices.

A generic graph

It’s also possible to define a new graph by writing a function that describes the edge set of the graph. This code example shows how to build a directed graph containing all edges (v, w) for which v is odd and w even.

// Define a graph by a function.
g := build.Generic(10, func(v, w int) bool {
    // Include all edges with v odd and w even.
    return v%2 == 1 && w%2 == 0
})

The build.Generic function returns a virtual graph with 10 vertices; its edge set consists of all edges (v, w), v ≠ w, for which the anonymous function returns true.

Implementation

Let’s start by looking at the main data type, a struct with five functions.

type Virtual struct {
	// The `order` field is, in fact, a constant function.
	// It returns the number of vertices in the graph.
	order int

	// The `edge` and `cost` functions define a weighted graph
	// without self-loops.
	//
	//  • edge(v, w) returns true whenever (v, w) belongs to
	//    the graph; the value is disregarded when v == w.
	//
	//  • cost(v, w) returns the cost of (v, w);
	//    the value is disregarded when edge(v, w) is false.
	//
	edge func(v, w int) bool
	cost func(v, w int) int64

	// The `degree` and `visit` functions can be used to improve
	// performance. They MUST BE CONSISTENT with edge and cost.
	// If not implemented, the `generic` or `generic0` implementation
	// is used instead. The `Consistent` test function should be used
	// to check compliance.
	//
	//  • degree(v) returns the outdegree of vertex v.
	//
	//  • visit(v) visits all neighbors w of v for which w ≥ a in
	//    NUMERICAL ORDER calling do(w, c) for edge (v, w) of cost c.
	//    If a call to do returns true, visit MUST ABORT the iteration
	//    and return true; if successful it should return false.
	//    Precondition: a ≥ 0.
	//
	degree func(v int) int
	visit  func(v int, a int,
		do func(w int, c int64) (skip bool)) (aborted bool)
}

Cycle graphs

As a simple example, here’s how to implement cycle graphs. A cycle graph of order n contains the edges {0, 1}, {1, 2}, {2, 3},… ,{n-1, 0}.

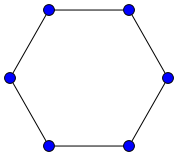
Cycle graph

Cycle graph of order 6

For a basic implementation of this class of graphs, we can write an edge function and use the generic implementation generic0 to fill in standard implementations of the other functions in the Virtual struct.

In the following code, g is a virtual circle graph of order n with edge costs equal to zero.

g := generic0(n, func(v, w int) (edge bool) {
	switch v - w {
	case 1 - n, -1, 1, n - 1:
		edge = true
	}
	return
})

The generic implementation of the degree function iterates over the n potential neighbors and calls the edge function for each one to check if it really is a neighbor. In this case, it’s trivial to compute the degree more efficiently:

// Precondition : n ≥ 3.
g.degree = func(v int) int { return 2 }

The generic implementation of the visit function also visits all potential neighbors. This can of course be done much more efficiently:

// Precondition : n ≥ 3.
g.visit = func(v int, a int,
	do func(w int, c int64) bool) (aborted bool) {
	var w [2]int
	switch v {
	case 0:
		w = [2]int{1, n - 1}
	case n - 1:
		w = [2]int{0, n - 2}
	default:
		w = [2]int{v - 1, v + 1}
	}
	for _, w := range w {
		if w >= a && do(w, 0) {
			return true
		}
	}
	return
}

Tensor product

Operators on virtual graphs are typically more complicated to implement, but they can be defined using the very same pattern. Here is an example showing how to implement the tensor product of two graphs.

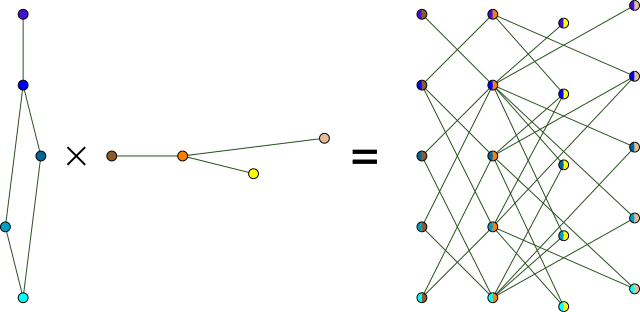
Tensor product

The tensor product of g1 and g2 is a graph whose vertices correspond to ordered pairs (v1, v2), where v1 and v2 are vertices in g1 and g2, respectively. The vertices (v1, v2) and (w1, w2) are connected by an edge whenever both of the edges {v1, w1} and {v2, w2} exist in the original graphs.

In the new graph, vertex (v1, v2) gets index n⋅v1 + v2, where n = g2.Order(), and index i corresponds to the vertex (i/n, i%n).

func (g1 *Virtual) Tensor(g2 *Virtual) *Virtual {
	m, n := g1.Order(), g2.Order()

	g := generic0(m*n, func(v, w int) (edge bool) {
		v1, v2 := v/n, v%n
		w1, w2 := w/n, w%n
		return g1.Edge(v1, w1) && g2.Edge(v2, w2)
	})

	g.degree = func(v int) (deg int) {
		v1, v2 := v/n, v%n
		return g1.degree(v1) * g2.degree(v2)
	}

	g.visit = func(v int, a int,
		do func(w int, c int64) bool) (aborted bool) {
		v1, v2 := v/n, v%n
		a1, a2 := a/n, a%n
		return g1.visit(v1, a1,
			func(w1 int, c int64) (skip bool) {
			if w1 == a1 {
				return g2.visit(v2, a2,
					func(w2 int, c int64) (skip bool) {
					return do(n*w1+w2, 0)
				})
			}
			return g2.visit(v2, 0,
				func(w2 int, c int64) (skip bool) {
				return do(n*w1+w2, 0)
			})
		})
	}
	return g
}

Code from tensor.go

Testing

Testing pure functions is typically straightforward – in this case it’s also a pure pleasure.

As always we need to check that the function calls produce the expected result, but the rest of the testing procedure can be fully automated. Given the edge and cost functions, the behavior of degree and visit are fully determined and can be automatically checked; it also works in reverse.

This is a blessing since the implementations tend to be quite different and often either edge or visit is considerably easier to implement than the other.

To test the Cycle function we simply need to check its output and call the automated consistency test:

for n := 0; n < 5; n++ {
	Consistent("Cycle", t, Cycle(n))
}

Performance

Iteration

The implementation of neighbor iteration is crucial for the performance of any graph library. Therefore all predefined building blocks and operations try to implement the visit function in time proportional to the actual number of neighbors.

However, with filter functions this is not possible. In particular, graphs built by the Generic function must visit all potential neighbors during iteration.

Caching

Caching can give large performance improvements but may be hard to automate. When and what to cache depends on many factors, including the actual data, hardware, and implementation.

Additionally, any graph, or part of a graph, which is described by a filter function function cannot be cached since we don’t know if the user-defined functions are pure – they may return different results given the same argument.

The solution is a function which activates caching for a specified component:

// Specific returns a cached copy of g with constant time
// performance for all basic operations. It uses space
// proportional to the size of the graph.
func Specific(g graph.Iterator) *Virtual

The implementation uses fixed precomputed lists to associate each vertex in the graph with its neighbors.

Not only can Specific be used to cache selected components, it can also be employed to import graphs that are represented by more traditional data structures.